
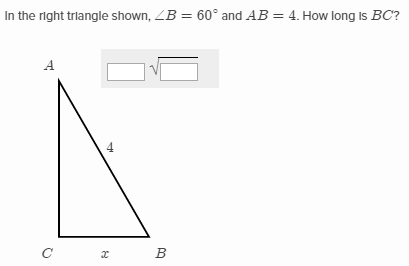
With the hypotenuse, we have information to determine the following: If you wanted to take a look at more examples of the 45 45 90 triangle, take a look at this interactive online reference for this special right triangle. Triangle ABC has side lengths 9, 40, and 41. You also happen to know a nice formula to figure out what the length of the hypotenuse is (the Pythagorean Theorem) and we'll show you how it will be used. Right Triangles Test Review Multiple Choice Identify the choice that best completes the statement or answers the question. Since you'll also find that this triangle is a right-angled triangle, we know that the third side that is not equal with the others is the hypotenuse. It is an isosceles triangle, with two equal sides. One of these triangles is the 45 45 90 triangle.

For a list of all the different special triangles you will encounter in math. These are the ones you'll most typically use in math problems as well. But for the ones that do, you will have to memorize their angles' values in tests and exams. There's not a lot of angles that give clean and neat trigonometric values. Special triangles take those long numbers that require rounding and come up with exact ratio answers for them. When numbers are rounded, it means that your answer isn't exact, and that's something that mathematicians do not like. Most trig questions you've done up till now have required that you round answers in the end. In this 45-45-90 triangle, I have been given a leg, so to find the other leg I. We have identified that these are important concepts to be introduced in geometry in order for students to access Algebra II and AP Calculus.Special triangles are a way to get exact values for trigonometric equations. There are several lessons in this unit that do not have an explicit common core standard alignment. These skills are critical for students' ability to understand calculus and integrals in future years. Although all right triangles have special features trigonometric functions and the Pythagorean theorem.The most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 triangles. From here, students describe how non-right triangles can be solved using the Law of Sines and Law of Cosines, in Topic E. This skill is extended in Topic D, the Unit Circle, where students are introduced to the unit circle and reference angles. Students gain practice with determining an appropriate strategy for solving right triangles. In Topic B, Right Triangle Trigonometry, and Topic C, Applications of Right Triangle Trigonometry, students define trigonometric ratios and make connections to the Pythagorean theorem. Students develop the algebraic tools to perform operations with radicals. Students use similarity to prove the Pythagorean theorem and the converse of the Pythagorean theorem. The ratios come straight from the Pythagorean theorem. Students define angle and side-length relationships in right triangles. Learn shortcut ratios for the side lengths of two common right triangles: 45°-45°-90° and 30°-60°-90° triangles. This unit begins with Topic A, Right Triangle Properties and Side-Length Relationships.
Students build an appreciation for how similarity of triangles is the basis for developing the Pythagorean theorem and trigonometric properties. In Unit 4, Right Triangles & Trigonometry, students develop a deep understanding of right triangles through an introduction to trigonometry and the Pythagorean theorem.


 0 kommentar(er)
0 kommentar(er)
